leetcode5_stack_and_queue
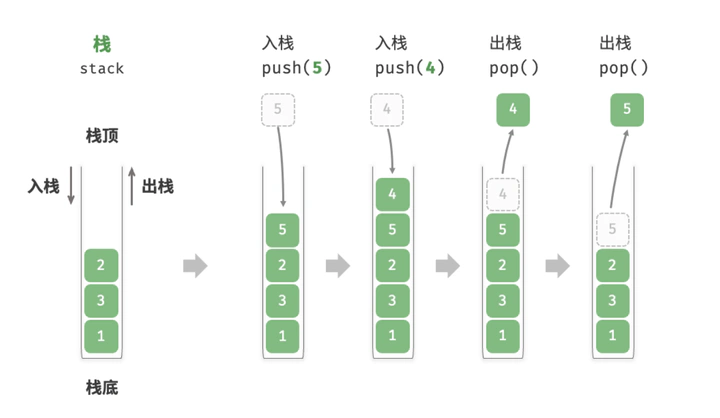
std::stack是一个容器适配器(container adapter),而不是容器(container)本身。它是建立在其他容器之上的一种封装,提供了一种LIFO(后进先出)的数据结构,其中元素的添加和移除只能在栈顶进行。
std::stack默认使用std::deque(双端队列)作为其底层容器,但也可以选择使用std::vector或std::list等其他容器作为底层实现。
我们也可以指定vector为栈的底层实现,初始化语句如下:
std::stack<int,std::vector<int>> v_stack; //使用vector为底层容器的栈
栈常见操作:push pop top empty
std::queue结构也类似,常见操作:push pop peek empty
双端队列 std::deque
priority_queue<Type, Container, Functional>;
Type是要存放的数据类型
Container是实现底层堆的容器,必须是数组实现的容器,如vector、deque
Functional是比较方式/比较函数/优先级
priority_queue<Type>;
此时默认的容器是vector,默认的比较方式是大顶堆less<type>
239滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
eg:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
【方法1:优先级队列】
一方面要排序,另一方面要记录元素位置,判断是否在窗口内。
排序队列,联想到优先级队列,标记元素位置,在队列中存放pair元素<nums[i],i>,标记位置。
移动窗口后,要插入新元素,还要循环判断队头元素的second是否在窗口内。
【方法2:双端队列】
显然,只要右面的某元素大于左侧,在之后的过程中,左侧不会成为窗口最大值,可以删去。
我们可以用队列存储还没被移除的数据下标,显然其对应的值是单调递减的。
推动窗口时,新元素进入队尾,不断弹出队尾的小值。(删去)
推动窗口时,检查队头是否出窗口,出则删去。
取最大值时,返回队头索引对应的值。
【方法3:分块和预处理】
以k为粒度对nums进行分组,并用两个数组记录每组内前i个与后i个数中最大值。
返回滑动窗口中最大值,即为前组后a个数最大值和后组前k-a个数最大值中较大者。
前面两种方法很多扣友说了,我来谈谈对第三种方法的理解,不得不说分块和预处理的方法真巧妙,题解说的前缀和后缀不太直观,我这里举个题目的例子来说明就好了,k=3。
preffix[i]存的是各个分组从分组开头到索引i的最大值(i % k == 0的值为各个分组的开头,这里对应是0,3,6),因为是从分组开头开始,所以是从左往右遍历,每次到分组的新的开头(进入新的分组),preffix[i]就直接更新为分组开头的元素,因为是从前往后遍历,所以是前缀最大值。看下面的例子:
suffix[i]存的是各个分组从分组末尾到索引i的最大值( (i + 1) % k == 0或最后一个索引的值为各个分组的末尾,这里对应是2,5,7),因为是分组末尾开始,所以是从右往左遍历,每次到分组的新的末尾(进入新的分组),suffix[i]就直接更新组为分组末尾的元素。因为是从后往前遍历,所以是后缀最大值。看下面的例子:
一个窗口最常见的情况是元素分别落入两个分组:落入两个分组时,前一个分组我们使用suffixMax[i]获得索引为i的前缀最大值(范围是i到这个分组的末尾,从右往左,对应是后缀),后一个分组我们使用prefixMax[i+k-1]获得索引为i+k-1的后缀最大值(范围是这个分组的开头到i+k-1,从左往右,对应是前缀),这两个值再比较得到的最大值就是整个窗口的最大值。
而另一种窗口的情况是元素落在一个分组里,这时候对应的suffixMax[i]的i是分组的开头,prefixMax[i+k-1]的i+k-1是这个分组的末尾,它们相当从两个方向对分组遍历获得了最大值,所以它们的值是一样的,这两个值再比较得到的最大值也是整个窗口的最大值。