数据结构（c++版）
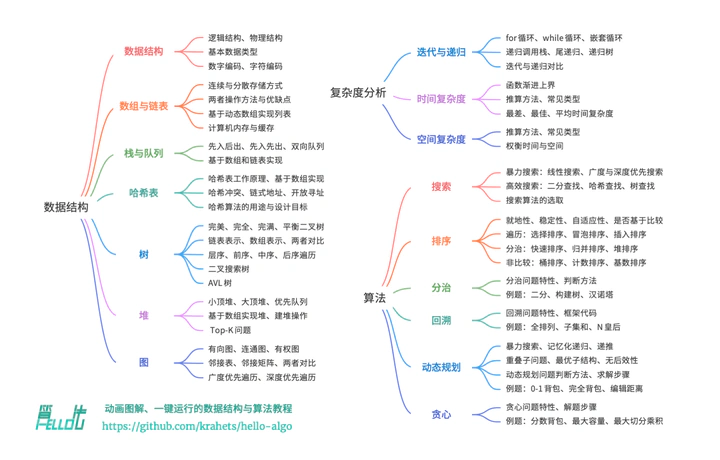Image credit:在刷leetcode的时候有一些点有些模糊， 特别针对复习一下。
主要集中于常见stl类的实现原理（结构，复杂度）和在c++中的使用。
c++指针/引用的明晰。stl数据结构的传递
附带总结一下常见算法及其写题模版。
参考https://www.hello-algo.com/
递归
**递归（recursion）**是一种算法策略，通过函数调用自身来解决问题。它主要包含两个阶段。
递：程序不断深入地调用自身，通常传入更小或更简化的参数，直到达到“终止条件”。
归：触发“终止条件”后，程序从最深层的递归函数开始逐层返回，汇聚每一层的结果。
而从实现的角度看，递归代码主要包含三个要素。
终止条件：用于决定什么时候由“递”转“归”。
递归调用：对应“递”，函数调用自身，通常输入更小或更简化的参数。
返回结果：对应“归”，将当前递归层级的结果返回至上一层。
观察以下代码，我们只需调用函数 recur(n) ，就可以完成 1+2+⋯+n 的计算：
/* 递归 */
int recur(int n) {
// 终止条件
if (n == 1)
return 1;
// 递：递归调用
int res = recur(n - 1);
// 归：返回结果
return n + res;
}
“调用栈”和“栈帧空间”这类递归术语已经暗示了递归与栈之间的密切关系。我们可以使用一个显式的栈来模拟调用栈的行为，从而将递归转化为迭代形式：
数据结构——内存连续性
分为连续空间存储（数组）和分散空间存储（链表）。物理结构从底层决定了数据的访问、更新、增删等操作方法，两种物理结构在时间效率和空间效率方面呈现出互补的特点。
基于数组可实现：栈、队列、哈希表、树、堆、图、矩阵、张量（维度 ≥3 的数组）等。
基于链表可实现：栈、队列、哈希表、树、堆、图等。
数组 arr[]
/* 初始化数组 */
// 存储在栈上
int arr[5];
int nums[5] = { 1, 3, 2, 5, 4 };
// 存储在堆上（需要手动释放空间）
int* arr1 = new int[5];
int* nums1 = new int[5] { 1, 3, 2, 5, 4 };
/* 访问元素，索引本质上是内存地址的偏移量 */
int randomNum = nums[Index];
/*数组元素在内存中是“紧挨着的”,插入元素后续需要依次位移（且扩容一下）在复杂的系统环境中，程序难以保证数组之后的内存空间是可用的，从而无法安全地扩展数组容量。因此在大多数编程语言中，数组的长度是不可变的。如果我们希望扩容数组，则需重新建立一个更大的数组，然后把原数组元素依次复制到新数组。这是一个 O(n) 的操作，在数组很大的情况下非常耗时
空间效率高：数组为数据分配了连续的内存块，无须额外的结构开销。
支持随机访问：数组允许在 O(1) 时间内访问任何元素。
插入与删除效率低：当数组中元素较多时，插入与删除操作需要移动大量的元素。
长度不可变：数组在初始化后长度就固定了，扩容数组需要将所有数据复制到新数组，开销很大。
空间浪费：如果数组分配的大小超过实际所需，那么多余的空间就被浪费了。
链表 listNode
链表的组成单位是节点（node）对象。每个节点都包含两项数据：节点的“值”和指向下一节点的“引用”。因此在相同数据量下，链表比数组占用更多的内存空间。
这里注意指针的应用，不要丢失链表，new新节点参考：
next->next = new listNode(),next = next->next;
列表 vector
当使用数组实现列表时，长度不可变的性质会导致列表的实用性降低。这是因为我们通常无法事先确定需要存储多少数据，从而难以选择合适的列表长度。若长度过小，则很可能无法满足使用需求；若长度过大，则会造成内存空间浪费。因此基于动态数组实现。
/* 初始化列表 */
// 需注意，C++ 中 vector 即是本文描述的 nums
// 无初始值
vector<int> nums1;
// 有初始值
vector<int> nums = { 1, 3, 2, 5, 4 };
//para为大小，初始化值
std::vector<int> v(10, 0);
/* 访问元素 */
int num = nums[1]; // 访问索引 1 处的元素
/* 更新元素 */
nums[1] = 0; // 将索引 1 处的元素更新为 0
/* 清空列表 */
nums.clear();
/* 在尾部添加元素 */
nums.push_back(1);
nums.push_back(3);
nums.push_back(2);
nums.push_back(5);
nums.push_back(4);
/* 在中间插入元素 */
nums.insert(nums.begin() + 3, 6); // 在索引 3 处插入数字 6
/* 删除元素 */
nums.erase(nums.begin() + 3); // 删除索引 3 处的元素
/* 排序列表 */
sort(nums.begin(), nums.end()); // 排序后，列表元素从小到大排列
//动态扩容时，分配更大内存块（通常两倍），然后拷贝所有内容（对于 push_back() 操作，通常只需在数组末尾插入新元素，时间复杂度为 O(1)。但当 vector 扩容时，会执行一次 内存分配和数据拷贝，导致单次操作的时间复杂度上升到 O(n)（n 为当前 vector 大小）。）
Q：在列表末尾添加元素是否时时刻刻都为 O(1) ？
如果添加元素时超出列表长度，则需要先扩容列表再添加。系统会申请一块新的内存，并将原列表的所有元素搬运过去，这时候时间复杂度就会是 O(n) 。
栈 stack
后入先出
/* 初始化栈 */
stack<int> stack;
/* 元素入栈 */
stack.push(1);
stack.push(3);
stack.push(2);
stack.push(5);
stack.push(4);
/* 访问栈顶元素 */
int top = stack.top();
/* 元素出栈 */
stack.pop(); // 无返回值
/* 获取栈的长度 */
int size = stack.size();
/* 判断是否为空 */
bool empty = stack.empty();
可以用链表（链表头栈顶）或数组（数组尾栈顶）实现栈。
时间
基于数组实现的栈在触发扩容时效率会降低，但由于扩容是低频操作，因此平均效率更高。
基于链表实现的栈可以提供更加稳定的效率表现。
空间
基于数组实现的栈可能造成一定的空间浪费。（二倍扩容未完全利用）
然而，由于链表节点需要额外存储指针，因此链表节点占用的空间相对较大。
std::stack 默认使用 std::deque 作为底层容器，但也可以使用 std::vector 或 std::list 来替换。
std::stack<int> s1; // 默认使用 std::deque
std::stack<int, std::vector<int>> s2; // 使用 std::vector 作为底层存储
队列 queue
先入先出
/* 初始化队列 */
queue<int> queue;
/* 元素入队 */
queue.push(1);
queue.push(3);
queue.push(2);
queue.push(5);
queue.push(4);
/* 访问队首元素 */
int front = queue.front();
/* 元素出队 */
queue.pop();
/* 获取队列的长度 */
int size = queue.size();
/* 判断队列是否为空 */
bool empty = queue.empty();
基于链表的实现：头出尾插，维护头尾指针，特殊判定空到首个节点
基于数组的实现，真实现头出要O（n），因此用一个front指针指向头，出时front++；头尾节点一直后移->使用环形数组->再补充扩容机制
二者对比类似栈。
std::queue 默认使用 std::deque 作为底层容器，
双向队列 deque
/* 初始化双向队列 */
deque<int> deque;
/* 元素入队 */
deque.push_back(2); // 添加至队尾
deque.push_back(5);
deque.push_back(4);
deque.push_front(3); // 添加至队首
deque.push_front(1);
/* 访问元素 */
int front = deque.front(); // 队首元素
int back = deque.back(); // 队尾元素
/* 元素出队 */
deque.pop_front(); // 队首元素出队
deque.pop_back(); // 队尾元素出队
/* 获取双向队列的长度 */
int size = deque.size();
/* 判断双向队列是否为空 */
bool empty = deque.empty();
双向队列的实现与队列类似，可以选择（双向）链表或（环形）数组作为底层数据结构。
Q：撤销（undo）和反撤销（redo）具体是如何实现的？
使用两个栈，栈 A 用于撤销，栈 B 用于反撤销。
每当用户执行一个操作，将这个操作压入栈
A，并清空栈B。当用户执行“撤销”时，从栈
A中弹出最近的操作，并将其压入栈B。当用户执行“反撤销”时，从栈
B中弹出最近的操作，并将其压入栈A。
优先级队列（见堆）
（无序容器）哈希表 unordered_map
hash表
用空间换取增删查都是O（1）的复杂度
/* 初始化哈希表 */
unordered_map<int, string> map;
/* 添加操作 */
// 在哈希表中添加键值对 (key, value)
map[12836] = "小哈";
map[15937] = "小啰";
map[16750] = "小算";
map[13276] = "小法";
map[10583] = "小鸭";
/* 查询操作 */
// 向哈希表中输入键 key ，得到值 value
string name = map[15937];
/* 删除操作 */
// 在哈希表中删除键值对 (key, value)
map.erase(10583);
/* 遍历哈希表 */
// 遍历键值对 key->value
for (auto kv: map) {
cout << kv.first << " -> " << kv.second << endl;
}
// 使用迭代器遍历 key->value
for (auto iter = map.begin(); iter != map.end(); iter++) {
cout << iter->first << "->" << iter->second << endl;
}
注意数组可以视作以index为key的哈希表。
可以用数组实现hash表，以key-value对为数组的一项（桶）（哈希表（buckets + 链表））
/* 键值对 */
struct Pair {
public:
int key;
string val;
Pair(int key, string val) {
this->key = key;
this->val = val;
}
};
/* 基于数组实现的哈希表 */
class ArrayHashMap {
private:
vector<Pair *> buckets;
public:
ArrayHashMap() {
// 初始化数组，包含 100 个桶
buckets = vector<Pair *>(100);
}
~ArrayHashMap() {
// 释放内存
for (const auto &bucket : buckets) {
delete bucket;
}
buckets.clear();
}
/* 哈希函数 */
int hashFunc(int key) {
int index = key % 100;
return index;
}
/* 查询操作 */
string get(int key) {
int index = hashFunc(key);
Pair *pair = buckets[index];
if (pair == nullptr)
return "";
return pair->val;
}
/* 添加操作 */
void put(int key, string val) {
Pair *pair = new Pair(key, val);
int index = hashFunc(key);
buckets[index] = pair;
}
/* 删除操作 */
void remove(int key) {
int index = hashFunc(key);
// 释放内存并置为 nullptr
delete buckets[index];
buckets[index] = nullptr;
}
/* 获取所有键值对 */
vector<Pair *> pairSet() {
vector<Pair *> pairSet;
for (Pair *pair : buckets) {
if (pair != nullptr) {
pairSet.push_back(pair);
}
}
return pairSet;
}
/* 获取所有键 */
vector<int> keySet() {
vector<int> keySet;
for (Pair *pair : buckets) {
if (pair != nullptr) {
keySet.push_back(pair->key);
}
}
return keySet;
}
/* 获取所有值 */
vector<string> valueSet() {
vector<string> valueSet;
for (Pair *pair : buckets) {
if (pair != nullptr) {
valueSet.push_back(pair->val);
}
}
return valueSet;
}
/* 打印哈希表 */
void print() {
for (Pair *kv : pairSet()) {
cout << kv->key << " -> " << kv->val << endl;
}
}
};
改良哈希表数据结构，使得哈希表可以在出现哈希冲突时正常工作。
仅在必要时，即当哈希冲突比较严重时，才执行扩容操作。
hash冲突
**法1:链式地址，**在原始哈希表中，每个桶仅能存储一个键值对。链式地址（separate chaining）将单个元素转换为链表，将键值对作为链表节点，将所有发生冲突的键值对都存储在同一链表中。（unordered_map使用此方法）
链式地址存在以下局限性。
占用空间增大：链表包含节点指针，它相比数组更加耗费内存空间。
查询效率降低：因为需要线性遍历链表来查找对应元素。值得注意的是，当链表很长时，查询效率 O(n) 很差。此时可以将链表转换为“AVL 树”或“红黑树”，从而将查询操作的时间复杂度优化至 O(logn) 。
法2:开放寻址（线行探测/平方探测/多次hash）
线性探测容易产生“聚集现象”。具体来说，数组中连续被占用的位置越长，这些连续位置发生哈希冲突的可能性越大，从而进一步促使该位置的聚堆生长，形成恶性循环，最终导致增删查改操作效率劣化。
值得注意的是，我们不能在开放寻址哈希表中直接删除元素。这是因为删除元素会在数组内产生一个空桶 None ，而当查询元素时，线性探测到该空桶就会返回，因此在该空桶之下的元素都无法再被访问到，程序可能误判这些元素不存在。为了解决该问题，我们可以采用懒删除（lazy deletion）机制：它不直接从哈希表中移除元素，而是利用一个常量 TOMBSTONE 来标记这个桶。在该机制下，None 和 TOMBSTONE 都代表空桶，都可以放置键值对。但不同的是，线性探测到 TOMBSTONE 时应该继续遍历，因为其之下可能还存在键值对。为此，考虑在线性探测中记录遇到的首个 TOMBSTONE 的索引，并将搜索到的目标元素与该 TOMBSTONE 交换位置。这样做的好处是当每次查询或添加元素时，元素会被移动至距离理想位置（探测起始点）更近的桶，从而优化查询效率。
与线性探测相比，多次哈希方法不易产生聚集，但多个哈希函数会带来额外的计算量。
hash扩容
当key过多时会出现负载较大（负载因子大），冲突较多，一般有阈值，复杂因子达到一定限度对hash表进行扩容。
编程语言通常会为数据类型提供内置哈希算法，用于计算哈希表中的桶索引。通常情况下，只有不可变对象是可哈希的。（类对象通常用地址为key进行hash）
unordered_set，时间负载度为O（1）的无序集合，类似实现。
有序关联容器（红黑树 近似AVL） map
相较于hash表，map中节点按key值排序，但增删查的开销变为O（logn）
底层为红黑树（自平衡二叉搜索树）
#include <iostream>
#include <map>
using namespace std;
int main() {
map<int, string> myMap; // 定义一个 key 为 int, value 为 string 的 map
// 插入元素
myMap[1] = "Apple";
myMap[3] = "Cherry";
myMap[2] = "Banana";
myMap[4] = "Dragonfruit"; // 存在 key=4，修改值；不存在，则创建
myMap.insert({5, "Elderberry"});//如果key=5已存在，不会修改其值
myMap.emplace(6, "Fig");//使用emplace插入，避免额外拷贝
// 遍历（默认按 key 递增排序）
for (const auto &pair : myMap) {
cout << pair.first << " -> " << pair.second << endl;
}
myMap.erase(2); // 删除 key=2
auto it = myMap.find(3);//迭代器删除
if (it != myMap.end()) {
myMap.erase(it);
}
return 0;
}
//自定义降序
map<int, string, greater<int>> descMap;
不允许重复 key，如果需要重复 key，请用 std::multimap。
有序集合容器 set各方面性能和map近似，但只有key，没有value。
树 tree，没有stl，需要手搓节点
/* 二叉树节点结构体 */
struct TreeNode {
int val; // 节点值
TreeNode *left; // 左子节点指针
TreeNode *right; // 右子节点指针
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
完美二叉树（perfect binary tree）所有层的节点都被完全填满。
完全二叉树（complete binary tree）只有最底层的节点未被填满，且最底层节点尽量靠左填充。
完满二叉树（full binary tree）除了叶节点之外，其余所有节点都有两个子节点。
平衡二叉树（balanced binary tree）中任意节点的左子树和右子树的高度之差的绝对值不超过 1 。
层序遍历（可以通过队列实现）
前序/中序/后序遍历（递归实现比较方便）
数组表示二叉树：父节点索引与子节点索引之间的“映射公式”：若某节点的索引为 i ，则该节点的左子节点索引为 2i+1 ，右子节点索引为 2i+2 。不完全的二叉树空位用none（或INT_MAX）
二叉搜索树左小右大，二叉搜索树的中序遍历序列是升序的。二叉搜索树增删改都是O（logn），其特殊变种（近似平衡二叉搜索树：红黑树）常用于有序容器的实现（set，map）
不进行平衡操作的话，二叉搜索树可能退化为有序链表：平衡二叉搜索树（AVL树）——通过左/右/左右/右左旋实现
==：用来比较两个变量是否指向同一个对象，即它们在内存中的位置是否相同。equals()：用来对比两个对象的值是否相等。
堆（优先级队列 priority_queue）
许多编程语言提供的是优先队列（priority queue），这是一种抽象的数据结构，定义为具有优先级排序的队列。
实际上，堆通常用于实现优先队列，大顶堆相当于元素按从大到小的顺序出队的优先队列。从使用角度来看，我们可以将“优先队列”和“堆”看作等价的数据结构。
/* 初始化堆 */
// 初始化小顶堆
priority_queue<int, vector<int>, greater<int>> minHeap;
// 初始化大顶堆
priority_queue<int, vector<int>, less<int>> maxHeap;
/* 元素入堆 */
maxHeap.push(1);
maxHeap.push(3);
maxHeap.push(2);
maxHeap.push(5);
maxHeap.push(4);
/* 获取堆顶元素 */
int peek = maxHeap.top(); // 5
/* 堆顶元素出堆 */
// 出堆元素会形成一个从大到小的序列
maxHeap.pop(); // 5
maxHeap.pop(); // 4
maxHeap.pop(); // 3
maxHeap.pop(); // 2
maxHeap.pop(); // 1
/* 获取堆大小 */
int size = maxHeap.size();
/* 判断堆是否为空 */
bool isEmpty = maxHeap.empty();
/* 输入列表并建堆 */
vector<int> input{1, 3, 2, 5, 4};
priority_queue<int, vector<int>, greater<int>> minHeap(input.begin(), input.end());
堆的实现：用数组表示完全二叉树。
插入元素时，我们首先将其添加到堆底。添加之后，由于 val 可能大于堆中其他元素，堆的成立条件可能已被破坏，因此需要修复从插入节点到根节点的路径上的各个节点，这个操作被称为堆化（heapify）。
/* 元素入堆 */
void push(int val) {
// 添加节点
maxHeap.push_back(val);
// 从底至顶堆化
siftUp(size() - 1);
}
/* 从节点 i 开始，从底至顶堆化 */
void siftUp(int i) {
while (true) {
// 获取节点 i 的父节点
int p = parent(i);
// 当“越过根节点”或“节点无须修复”时，结束堆化
if (p < 0 || maxHeap[i] <= maxHeap[p])
break;
// 交换两节点
swap(maxHeap[i], maxHeap[p]);
// 循环向上堆化
i = p;
}
}
堆顶元素出堆时（pop）：
交换堆顶元素与堆底元素（交换根节点与最右叶节点）。
交换完成后，将堆底从列表中删除（注意，由于已经交换，因此实际上删除的是原来的堆顶元素）。
从根节点开始，从顶至底执行堆化。（将根节点的值与其两个子节点的值进行比较，将最大的子节点与根节点交换。然后循环执行此操作，直到越过叶节点或遇到无须交换的节点时结束。）
/* 元素出堆 */
void pop() {
// 判空处理
if (isEmpty()) {
throw out_of_range("堆为空");
}
// 交换根节点与最右叶节点（交换首元素与尾元素）
swap(maxHeap[0], maxHeap[size() - 1]);
// 删除节点
maxHeap.pop_back();
// 从顶至底堆化
siftDown(0);
}
/* 从节点 i 开始，从顶至底堆化 */
void siftDown(int i) {
while (true) {
// 判断节点 i, l, r 中值最大的节点，记为 ma
int l = left(i), r = right(i), ma = i;
if (l < size() && maxHeap[l] > maxHeap[ma])
ma = l;
if (r < size() && maxHeap[r] > maxHeap[ma])
ma = r;
// 若节点 i 最大或索引 l, r 越界，则无须继续堆化，跳出
if (ma == i)
break;
swap(maxHeap[i], maxHeap[ma]);
// 循环向下堆化
i = ma;
}
}
常用场景：获取最大的k个。（top-k -> nlogk）
依次入堆并堆化的操作复杂度为nlogn
n复杂度的建堆：见遍历造树，然后按层序遍历的倒序堆化
图（）
图遍历：
广搜：类似树的层序遍历，借用队列，但需要靠visited数组防止重复遍历。
/* 广度优先遍历 */
// 使用邻接表来表示图，以便获取指定顶点的所有邻接顶点
vector<Vertex *> graphBFS(GraphAdjList &graph, Vertex *startVet) {
// 顶点遍历序列
vector<Vertex *> res;
// 哈希集合，用于记录已被访问过的顶点
unordered_set<Vertex *> visited = {startVet};
// 队列用于实现 BFS
queue<Vertex *> que;
que.push(startVet);
// 以顶点 vet 为起点，循环直至访问完所有顶点
while (!que.empty()) {
Vertex *vet = que.front();
que.pop(); // 队首顶点出队
res.push_back(vet); // 记录访问顶点
// 遍历该顶点的所有邻接顶点
for (auto adjVet : graph.adjList[vet]) {
if (visited.count(adjVet))
continue; // 跳过已被访问的顶点
que.push(adjVet); // 只入队未访问的顶点
visited.emplace(adjVet); // 标记该顶点已被访问
}
}
// 返回顶点遍历序列
return res;
}
深搜：类似树的深度遍历，递归回溯，同样靠visited数组防止重复遍历（回visited）
/* 深度优先遍历辅助函数 */
void dfs(GraphAdjList &graph, unordered_set<Vertex *> &visited, vector<Vertex *> &res, Vertex *vet) {
res.push_back(vet); // 记录访问顶点
visited.emplace(vet); // 标记该顶点已被访问
// 遍历该顶点的所有邻接顶点
for (Vertex *adjVet : graph.adjList[vet]) {
if (visited.count(adjVet))
continue; // 跳过已被访问的顶点
// 递归访问邻接顶点
dfs(graph, visited, res, adjVet);
}
}
/* 深度优先遍历 */
// 使用邻接表来表示图，以便获取指定顶点的所有邻接顶点
vector<Vertex *> graphDFS(GraphAdjList &graph, Vertex *startVet) {
// 顶点遍历序列
vector<Vertex *> res;
// 哈希集合，用于记录已被访问过的顶点
unordered_set<Vertex *> visited;
dfs(graph, visited, res, startVet);
return res;
}
相较于线性关系（链表）和分治关系（树），网络关系（图）具有更高的自由度，因而更为复杂。
当邻接表中的链表过长时，可以将其转换为红黑树或哈希表，从而提升查询效率。
